Metode heuristik dalam penentuan rute
Permasalahan penentuan rute biasanya merupakan permasalahan NP-Hard Problem dimana penyelesaian dengan metode exact seringkali akan memakan waktu yang cukup lama untuk menyelesaikannya. Karena sebab inilah banyak para ahli yang merancang penyelesaian suatu problem dengan menggunakan merode heuristik. Metode Heuristik adalah teknik yang dirancang untuk memecahkan masalah yang mengabaikan apakah solusi dapat dibuktikan benar, tapi yang biasanya menghasilkan solusi yang baik atau memecahkan masalah yang lebih sederhana yang mengandung atau memotong dengan pemecahan masalah yang lebih kompleks. Metode Heuristik ini bertujuan untuk mendapatkan performa komputasi atau penyederhanaan konseptual, berpotensi pada biaya keakuratan atau presisi. Metode heuristik ada dua jenis yakni metode heuristik sederhana dan metaheuristik. Metode heuristik contohnya adalah cheapest insertion, Priciest Insertion, Nearest insertion, Farthest Insertion, Nearest addition dan Clarke and Wright Saving Method. Adapun penjelasannya sebagai berikut :
1) Cheapest insertion hal pertama kali yang dilakukan adalah menentukan setiap titik yang masih tersisa dan bebas atau titik yang belum dikunjungi yang menghasilkan link optimal untuk menyisipkan titik ini. Ini sesuai dengan minimisasi pertama dalam persamaan:
Penalti penyisipan adalah jumlah jarak ke titik bebas dikurangi jarak dari link yang akan dihapus. Pada Cheapest insertion kemudian dilakukan pemilihan titik untuk disisipkan sebagai titik penyisipan dengan penalti minimum.
2) Pada Priciest insertion yang dilakukan pertama kali adalah menentukan setiap titik yang masih tersisa dan bebas atau titik yang belum dikunjungi yang menghasilkan link optimal untuk menyisipkan titik ini. Ini sesuai dengan minimisasi pertama dalam persamaan:
Identik dengan proses cheapest insertion, penalti penyisipan adalah jumlah jarak ke titik bebas dikurangi jarak dari link yang akan dihapus. Pricest Insertion kemudian dipilih titik untuk disipkan sebagai titik penyisipan dengan penalti maksimum.
3) Pada Nearest insertion yang dilakukan pertama kali adalah menentukan titik untuk disipkan dengan mencari titik bebas yang paling dekat dengan suatu titik pada tur. Algoritma pada dasarnya melakukan sebuah operasi mini-min pada jarak dari titik bebas untuk suatu titik pada tur.
Selanjutnya dengan algoritma ini, ditentukan link terbaik untuk menyisipkan titik ini. Proses ini identik dengan proses pada cheapest insertion dan farthest insertion.
4) Pada farthest insertion yang dilakukan pertama kali adalah menentukan setiap titik bebas yang memiliki jarak ke titik manapun pada tur terkecil. Kemudian masukkan titik bebas yang memiliki maksimum jarak terkecil ke titik pada tur. Algoritma ini pada dasarnya merupakan sebuah operasi maxi-mnt pada jarak dari titik bebas untuk suatu titik pada tur.
Selanjutnya ditentukan link terbaik untuk menyisipkan titik ini. Proses ini identik dengan proses pada cheapest insertion dan farthest insertion.
5) Pada Nearest addition yang pertama kali dilakukan adalah menentukan titik yang akan disisipkan dengan mencari titik bebas yang paling dekat dengan suatu titik pada tur.
 Selanjutnya ditentukan link terbaik untuk menyisipkan titik ini dengan memeriksa dua link pada insiden tur ke titik tur paling dekat dengan titik bebas tersebut. Ini merupakan pencarian yang lebih terbatas dibanding dengan proses pada cheapest insertion dan farthest insertion
Selanjutnya ditentukan link terbaik untuk menyisipkan titik ini dengan memeriksa dua link pada insiden tur ke titik tur paling dekat dengan titik bebas tersebut. Ini merupakan pencarian yang lebih terbatas dibanding dengan proses pada cheapest insertion dan farthest insertion

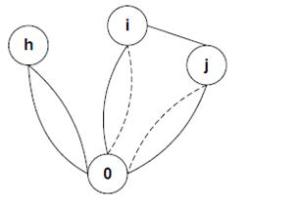
6) Clarke dan Wright (1964) mengembangkan prosedur konstruksi yang memanjang sebagian rute atau rute primitif pada dua titik akhir. Secara konseptual algoritma mendefinisikan titik pangkal dan menbangun sebuah tur Eulerian yang memiliki pengertian mengunjungi masing-masing titik lain dan kemudian kembali ke pangkal. Tur Eulerian kemudian dikurangi panjangnya dengan mencari jalan dengan saving terbesar. Saving dihitung sebagai jumlah dari jarak ke titik dasar dari dua titik dikuranigi jarak antara dua titik.
Gambar Ilustrasi Clarke and Wright Tour Extension
Setelah dua titik telah bergabung, titik tersebut tiidak akan pernah dipisahkan lagi oleh algoritma Clarke dan Wright. Serial varian dari algoritma memperluas parsial satu rute di ujungnya titik, yang tersambung ke titik pangkal. Titik berikutnya kemudian dipilih dengan mencari titik dengan saving terbesar untuk saat ini titik akhir dari tur parsial.

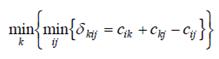
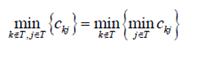

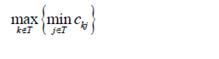

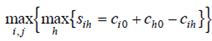

Jworok banget tulisannya. Hehehe…
Tapi mantaplahh…
January 21, 2010 at 3:23 PM
maaf, kalo boleh di share itu argumennya ngambil dari buku/dari mana?
April 25, 2016 at 4:37 AM